Proyectos de Investigación en Inteligencia Artificial Aplicada
Perfilado de sección
-
Proyecto de Investigación en Inteligencia Artificial Aplicada
Universidad Tecnológica Nacional
Facultad Regional Haedo
Idioma
Esta página web está disponible en inglés
 y castellano
y castellano  .
.
Descripción
La inteligencia artificial hace uso de las computadoras para aumentar las capacidades matemáticas y lógicas humanas. Este proyecto de investigación busca automatizar las habilidades humanas. Por otra parte, es necesario incentivar a los estudiantes de grado a una investigación temprana y a partir de los resultados obtenidos de sus investigaciones generar contenido educativo.
Objetivos de esta investigación
El ensayo no destructivo por visión artificial aplicado a materiales metálicos puede complementar a otras técnicas de inspección, para minimizar los errores de diagnóstico. Por otro lado, el aprendizaje profundo, por ejemplo, aplicado a la visión artificial, busca construir modelos matemáticos que aprendan de las imágenes que contienen fisuras u otro tipo de daño superficial. Los grandes volúmenes de datos que deben analizar las redes neuronales artificiales requieren de algoritmos específicos eficientes.
-
Proyecto de investigación y desarrollo UTN
PID 8268: "Sistema de detección y evaluación de fisuras superficiales en materiales metálicos basado en cámaras de visión artificial". Vigencia 01/01/2021 a 31/12/2023. Homologado.
PID 8706: "Detección y clasificación de defectos en rieles usando algoritmos de aprendizaje profundo en GPU". Vigencia 01/04/203 a 31/03/2025. Homologado.
Objetivos de esta investigación
El ensayo no destructivo por visión artificial aplicado a materiales metálicos puede complementar a otras técnicas de inspección, para minimizar los errores de diagnóstico. Por otro lado, el aprendizaje profundo, por ejemplo, aplicado a la visión artificial, busca construir modelos matemáticos que aprendan de las imágenes que contienen fisuras u otro tipo de daño superficial. Los grandes volúmenes de datos que deben analizar las redes neuronales artificiales requieren de algoritmos específicos eficientes. Para dar respuestas a estos planteos es que se establecieron los siguientes objetivos:
Objetivos generales
✅ Generar algoritmos específicos que se ejecuten en hardware dedicado para la detección y evaluación de daños superficiales en materiales metálicos mediante la técnica de ensayo no destructivo por visión artificial.
Objetivos específicos
✅ Establecer las técnicas de procesamiento de imágenes y aprendizaje profundo para aplicar el ensayo no destructivo por visión artificial.
✅Profundizar el estudio de la defectología en la cual el método de visión artificial puede ofrecerse como un complemento necesario.
✅ Establecer el conjunto de datos para el entrenamiento de la red neuronal artificial.
✅ Desarrollar capacidades de programación e implementación en el lenguaje de programación adecuados para el requerimiento.
✅ Interpretar los resultados producto del uso de la red neuronal artificial entrenada; con el fin de poder predecir la defectología estudiada.
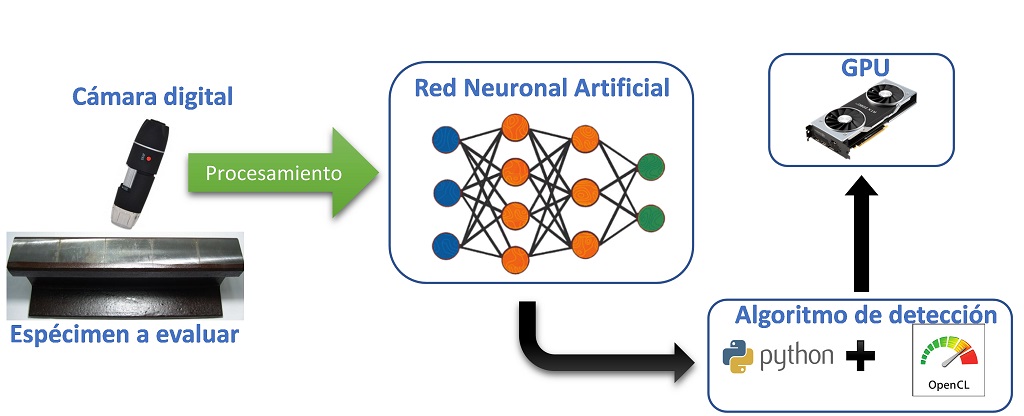
Esquema de detección de fisuras
En este primer año de trabajo, estamos estudiando y aplicando los algoritmos conocidos como perceptrón, perceptrón multicapa, y redes convolucionales. A continuación se muestra la figura resumen que sintetiza las diferentes etapas de investigación.

Actividades: 0 -
Perceptrón
Los estudiantes que forman parte del proyecto de investigación y desarrollo han escrito una colección de ejemplos en Python Jupyter Notebook para demostrar el funcionamiento del perceptrón. Para caracterizar el funcionamiento del perceptrón lograron clasificar compuertas lógicas (AND y OR) de dos entradas. En este contexto, aprenden habilidades en inteligencia artificial y en programación, mientras crean contenido para compartir a los estudiantes de las carreras de grados que se dictan en Universidad Tecnológica Nacional - Facultad Regional Haedo.
Actividades: 0 -
Introduction
Esta sección tiene como propósito explicar el algoritmo de aprendizaje perceptrón [1] ,propuesto originalmente por Frank Rosenblatt en 1958, luego refinado y cuidadosamente analizado por Minsky y Papert [2] en 1969. Además, se explicará el modelo neuronal McCulloch-Pitts [3] publicado en 1943, que posteriormente evoluciona al modelo de aprendizaje propuesto por [1].
Actividades: 0 -
Evolución del perceptrón
Modelo McCulloch-Pitts
El modelo que propone McCulloch-Pitts [3] tiene una estructura y comportamiento simplificado de una neurona fisiológica, Fig. 1.a, comúnmente llamado modelo bioinspirado. La Red Neuronal Biológica (RNB) presenta dendritas, que son las encargadas de recibir los estímulos de otras neuronas, luego trasmite esta información al cuerpo celular regulando su intensidad. El cuerpo celular se encarga de sumar las características anteriores para generar una señal eléctrica, que de acuerdo con el umbral del potencial de acción dado por las diferentes concentraciones de iones Na+, K+ y Cl− genera un disparo hacia otras neuronas. En el caso de superar el umbral del potencial de disparo, el axón transmite la señal eléctrica generada en el cuerpo celular a otras neuronas a través de las sinapsis. El modo de funcionamiento antes mencionado, a modo de ejemplo, es replicado por un perceptrón en forma artificial, donde en la figura 1.b se puede ver las mismas partes que forman parte del modelo biológico. El modelo de Red Neuronal Artificial (RNA) consiste en entradas (dendritas) que se propagan por los coeficientes (sinapsis). La combinación lineal, Ec. 1 (cuerpo celular) entre las entradas y los pesos sinápticos confluye en una operación no lineal denominada función de activación (axón).
$$ \color{orange} {S=\sum_{i=1}^{n}{w_i\ast x_i} \quad (1)} $$
Un perceptrón toma varias entradas binarias x1, x2, etc y produce una sola salida binaria. Los coeficientes W son números reales que expresa la importancia de la respectiva entrada con la salida. La salida de la neurona será 1 ó 0 si la suma de la multiplicación de los coeficientes por entradas es mayor o menor a un determinado umbral.
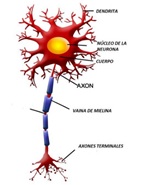
(a) Neurona biológica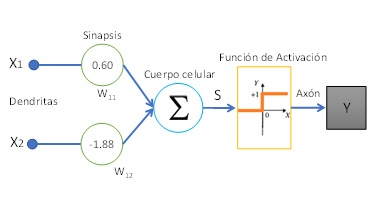
(b) Modelo McCulloch-PittsFigura 1: Comparación entre una neurona biológica y artificial
Función de activación propuesta por McCulloch-Pitts
En la figura 1.b se aprecia que entre la salida del cuerpo celular (S) y la salida (Y) existe una función de activación \( (\varphi\left(S\right)) \) $$ \color{orange} { \varphi\left(S\right) =\begin{cases}1 & S \geq 0\\0 & S <0\end{cases} \quad (2)} $$
Modelo Rosenblatt
Frank Rosenblatt [1] inspirado en el trabajo propuesto por sus colegas McCulloch-Pitts [3] desarrollo el concepto de perceptrón. El perceptrón introduce algunos cambios al modelo explicado en la sección 2.1. Uno de los cambios que propone es introducir una entrada adicional X0 que tendrá un valor fijo en 1 con el coeficiente W0. Al adicionar estos nuevos parámetros es lo mismo a agregar un sesgo a la combinación lineal de la Ec. 1. Por tal motivo, la Ec.1 se convierte en la Ec. 3, y como se observa el limite inferior de la sumatoria comienza desde i=0.
$$ \color{orange} { S=\sum_{i=0}^{n}{w_i\ast x_i} \quad (3) }$$
El otro cambio que realiza [1], consiste en cambiar la función de activación denominada función signo. En este caso, la función genera un 0, -1 o 1 en su salida de acuerdo con el valor de S, Ec. 4.
$$ \color{orange} {\varphi\left(S\right) =\begin{cases}1 & S>0 \\0 & S=0 \\-1 & S <0\end{cases} \quad (4)} $$Actividades: 0 -
Enseñar para que aprenda
Para que el perceptrón pueda aprender es necesario enseñarle lo que debe recordar. Este tipo de aprendizaje se lo denomina aprendizaje asistido, ya que, es una técnica que permite entrenar la RNA a partir de un conjunto de datos para que logre una salida deseada. Es necesario remarcar que los datos de entradas deben ser linealmente separable, ya que, este método es para una clasificación del tipo binaria. Para actualizar los valores de los pesos sinápticos W, se puede definir la Ec. 5.
$$ \color{orange} { \mathbf{{W}_{nuevo}} = \mathbf{{W}_{anterior}}+\mathbf{{Y}_{d}}.\mathbf{X} \quad (5)} $$
\( \color{orange} {\ Donde: \\ \; \\ \mathbf{{W}_{new}} \text{ : Vector of synaptic weights updated} \\ \mathbf{{W}_{old}} \text{ : Vector of prior synaptic weights.}\\ \mathbf{{Y}_{d}} \text{ : Desired output vector.}\\ \mathbf{X} \text{ : Input vector.}} \)
La regla de actualización presentada en la Ec. 5 es válida si las etiquetas son {-1, 1}. Por ejemplo, si tenemos el siguiente escenario:
$$ \color{orange} { \begin{cases}{W}_{0}= 0 +(-1*-1) \\ {W}_{1}=0 +(-1*\;\; 1\;)\end{cases} \quad (6)} $$
Cuando se aplica la Ec. (5) para las condiciones de entrada y salida, permitirá que los coeficientes w0 y w1 cambien la dirección de la actualización, Ec. 6. Pero, en el caso que la etiquetas sean {0, 1} y exista una clasificación incorrecta de la entrada X y su verdadero valor sea 0, entonces los coeficientes nunca serán actualizados, Ec. 7.
$$ \color{orange} { \begin{cases}{W}_{0}= 0 +(0*1) \\ {W}_{1}=0 +(0*1)\end{cases} \quad (7)} $$
Para solucionar este inconveniente, y poder generalizar tanto para {-1, 1} y {0, 1} y lograr que aprenda se puede proponer otra regla de actualización, Ec. 8.
$$ \color{orange} { \mathbf{{W}_{nuevo}}=\mathbf{{W}_{anterior}}+(\mathbf{{Y}_{d}-{Y}_{e}}).\mathbf{X} \quad (8)} $$
\( \color{orange} {\ Donde: \\ \; \\ \mathbf{{W}_{new}} \text{ : Vector of synaptic weights updated}\\ \mathbf{{W}_{old}} \text{ : Vector of prior synaptic weights.}\\ \mathbf{{Y}_{d}} \text{ : Desired output vector.}\\ \mathbf{{Y}_{e}} \text{ : Vector of the estimated output}\\ \mathbf{X} \text{ : Input vector.}} \)
The change in Eq. 8 lies in adopting an error that is made up of the difference between the desired output and the corresponding estimated output by combining Eq. 3 and Eq. 2 or Eq. 3 and Eq. 4. In this context, it can be said if the labels are {0, 1}, when the perceptron classifies correctly, the error will be 0. Therefore, it will not be necessary to change the coefficients W. In the scenario where the labels are {-1, 1 }, the error will be 0 if the classification is correct, and in the case of incorrect classification it will be 2 or -2 and the direction of updating the coefficients can be changed.
Actividades: 0 -
Función de pérdida
Es necesario saber si el perceptrón aprendió, para ello se emplea una función denominada función de pérdida (en inglés loss function). Esta función indica si el modelo acertó las predicciones, es decir, un valor bajo y en el caso de no lograr clasificar en forma correcta se tendrá un valor alto. Cuando el perceptrón aprendió correctamente todas las entradas la función de pérdida es cero. Una función de pérdida muy utilizada es la suma de los errores cuadráticos (en inglés sum of squared errors) expresada en la Ec. 9.
$$ \color{orange} { \sum_{i=0}^{n}(y_{d_i}-y_{e_i})^2 \quad (9) }$$
\( \color{orange} {\ Donde: \\ \; \\ y_{d} \ : \ Valor \ de \ la \ salida \ deseada. \\ y_{e} \ : \ Valor \ de \ la \ salida \ estimada} \)
Actividades: 0 -
Implementación en Python
Descripción
Esta sección proporciona una breve introducción al algoritmo de perceptrón y al conjunto de datos de la compuerta lógica AND que usaremos en este tutorial. NOTA: Se sugiere modificar el algoritmo para obtener el conjunto de datos de entrenamiento en forma estocástica.
Inicialización
import pandas as pd import numpy as np data = [[-1,-1, 1,-1], [-1, 1, 1,-1], [ 1,-1, 1,-1], [ 1, 1, 1, 1]] pd.DataFrame(data, index=list(range(len(data))), columns=['X1', 'X2','bias','Y'])Cálculo de la salida
### Ver sección "2.2 Evolución del perceptrón"### prediction = sign(np.dot(weight, training))Función de activación
### Ver sección "2.2 Evolución del perceptrón"### def sign(x): if x > 0: return 1.0 elif x < 0: return -1.0 else: return 1.0Cálculo del error
### Ver sección "2.4 Función de pérdida"### error = desired - prediction sse += error**2Actualización de los pesos
### Ver sección "2.3 Enseñar para que aprenda"### weight = weight + error * trainingAlgoritmo Completo
def sign(x): if x > 0: return 1.0 elif x < 0: return -1.0 else: return 1.0 import pandas as pd import numpy as np data = [[-1,-1, 1,-1], [-1, 1, 1,-1], [ 1,-1, 1,-1], [ 1, 1, 1, 1]] pd.DataFrame(data, index=list(range(len(data))), columns=['X1', 'X2','bias','Y']) train_data = pd.DataFrame(data, index=list(range(len(data))), columns=['X1', 'X2','bias','Y']) train_Y = train_data.Y train_data = train_data[['X1', 'X2','bias']] train_data.head() weight = np.zeros(train_data.shape[1]) for epoch in range(100): sse = 0.0 for sample in range(train_data.shape[0]): training = train_data.loc[sample].values desired = train_Y.loc[sample] prediction = sign(np.dot(weight, training)) error = desired - prediction sse += error**2 weight = weight + error * training print(f'SSE: {sse}') if sse == 0: break print(f'Weights: {weight}, Epoch: {epoch+1}')Actividades: 0 -
References
[1] Rosenblatt, F. (1958). The perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review, 65(6), 386–408. https://doi.org/10.1037/h0042519
[2] Minsky, M., Papert, S. (1969). Perceptrons: An Introduction to Computational Geometry, MIT Press, Cambridge, MA, USA. https://doi.org/10.1126/science.165.3895.780
[3] McCulloch, W.S., Pitts, W. A. (1943). Logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics 5, 115–133. https://doi.org/10.1007/BF02478259
[4] Alan V. Oppenheim and Ronald W. Schafer. 2009. Discrete-Time Signal Processing (3rd. ed.). Prentice Hall Press, USA.Actividades: 0 -
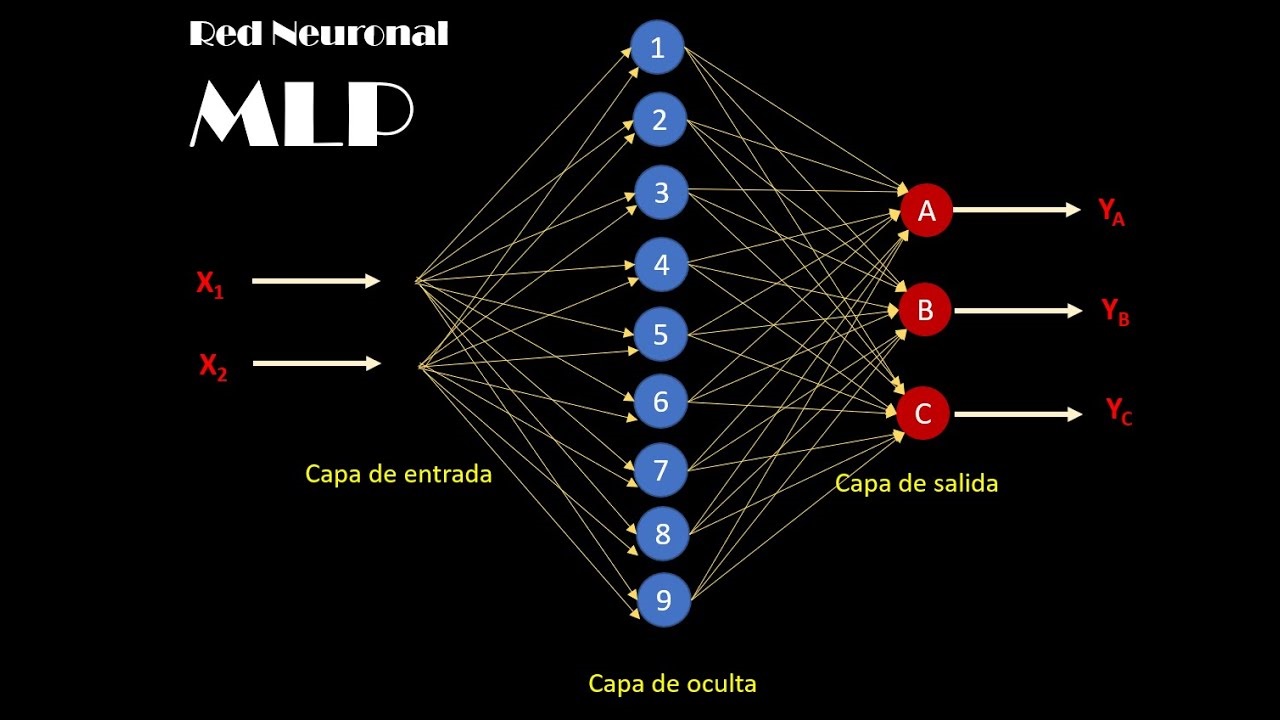
Multilayer Perceptron
 Actividades: 0
Actividades: 0 -
MLP para la compuerta XOR
🎙️Claudio Acuña
El objetivo de este ejemplo consiste en implementar un perceptrón multicapa totalmente conectado para que aprenda una compuerta lógica XOR de dos entradas. En la animación se puede observar como la RNA clasifica las entradas etiquetadas como {-1,1} según su salida {-1,1}. La RNA, bajo estas condiciones, separa las salidas mediante rectas de decisión. El algoritmo de aprendizaje implementado es conocido como retropropagación (en inglés backpropagation). En este sentido, los alumnos estudiaron la matemática que hay detrás del gradiente descendente para minimizar la función cuadrática de pérdida (en inglés squared error loss). Además, es posible observar en la animación la evolución de los pesos “V” en cada época (en inglés epoch), que forman parte de la capa oculta. El criterio de detención del entrenamiento fue establecer un error menor a 0,05.
Actividades: 0 -
Modelo de regresión MLP
🎙️ Claudio Acuña
Varias personas piensan que las redes neuronales artificiales (RNA) son difíciles de entender, pero para nuestro equipo, este no es el caso en absoluto. En este video, exploramos cada etapa de una RNA y mostramos los resultados del entrenamiento usando una señal como conjunto de datos.
Actividades: 0 -
Procesamiento digital de imágenes
Los estudiantes que forman parte del proyecto de investigación y desarrollo han escrito una colección de ejemplos en Python Jupyter Notebook para demostrar el funcionamiento de diversos métodos de procesamiento digital de imágenes. Luego de analizar la literatura en este campo de conocimiento, los estudiantes implementaron transformaciones del espacio de color y filtrado mediante núcleos de convolución. En este contexto, aprenden habilidades en procesamiento digital de imágenes y en programación, mientras crean contenido para compartir a los estudiantes de las carreras de grados que se dictan en Universidad Tecnológica Nacional - Facultad Regional Haedo.
Actividades: 0 -
Espacio de color YIQ
🎙️Claudio Acuña
The YIQ color space is frequently used in digital image processing. One of the reasons is the ability to recover the Y component associated with the grayscale image.
Actividades: 0 -
Núcleos de convolución
🎙️ Claudio Acuña
Un núcleo de imagen es una matriz diminuta que se utiliza para crear efectos similares a los que se ven en Photoshop o Gimp, como desenfoque, nitidez, contorno y relieve. También se utilizan en el aprendizaje automático para la "extracción de características", que es un método para detectar las partes más relevantes de una imagen. En este contexto, el proceso se conoce más ampliamente como redes neuronales convolucionales (ConvNet).
Filtro Sobel
Los bordes son discontinuidades abruptas en una imagen que pueden ser causadas por el color de la superficie, la profundidad, la iluminación u otros factores. En este sentido, identificamos los bordes en la imagen de abajo donde hay un cambio repentino de intensidad.
 Actividades: 0
Actividades: 0 -
Redes neuronales convolucionales
En este video, creado por los integrantes del proyecto de investigación y desarrollo, explora el funcionamiento de una red neuronal convolucional desarrollada desde cero para el conjunto de datos MNIST. Tras programar cada etapa, los estudiantes comparten cómo funciona el entrenamiento para dígitos escritos a mano.
Stride
"Stride" en una red neuronal se refiere a la cantidad de pasos que toma el filtro o la ventana de convolución al moverse a través de la entrada. Un "Stride" más grande significa que el filtro se desplaza en incrementos mayores, reduciendo la resolución espacial de la salida y acelerando el proceso de convolución.
Cross-Correlation
Cross-Correlation" es un paso esencial en la convolución de redes neuronales. Representa la comparación punto a punto de dos conjuntos de datos, como un filtro y una porción de entrada. Este proceso destaca la presencia de patrones específicos y ayuda a la red a reconocer características importantes en los datos.
Max Pooling
"Max Pooling" es una técnica utilizada para reducir la dimensionalidad de una capa de convolución, conservando las características más relevantes. Consiste en seleccionar el valor máximo de una región específica de la capa de entrada. Esto ayuda a disminuir la carga computacional y a mejorar la invarianza a pequeñas traslaciones en la entrada.
Actividades: 0 -
Algoritmos
Los integrantes del proyecto de investigación y desarrollo utiliza Google Colab para ejecutar los algoritmos.
Modelo Descripción Google Colab Perceptrón El perceptrón es una modelo simplificado de una neurona biológica. 🚫 MLP Un perceptrón multicapa es una red neuronal artificial prealimentada que mapea un conjunto de datos de entrada en otro conjunto de datos de salida 🚫 🚫 Actividades: 0 -
Graduate students
Claudio Acuña Pavese, 2022, “Thickness gauge using the eddy current method”.
Technical summary
Non-destructive testing (NDT) by eddy currents (EC) is a reliable evaluation method that is applied in different areas such as nuclear, the petrochemical industry, air and rail transport, among others. The wide use of coating meters is known, both in different industries and in research and development laboratories. Generally, these devices are manufactured to perform measurements on a limited number of substrates, reducing the range of applications. In this context, the project aims to develop and implement artificial neural network (ANN) algorithms and build a functional prototype for field application in an embedded system. The sensor is composed of a Colpitts oscillator. The impedance of the resonator tank is modified according to the lift-off (in EC lift-off is called the separation between the probe and the component to be inspected), and this generates changes in the resonance frequency. The system calibration curve is determined through the variation of the resonance frequency as a function of the lift-off. Eddy currents method, like all NDT methods, is a comparative method that needs a calibration curve in order to be implemented. The sinusoidal signal coming from the probe enters the embedded system that will be in charge of conditioning it. In the next stage of the device, a calibration must be performed depending on the substrate being used. Calibration is performed by training an ANN, which will have the output frequency of the oscillator as data set according to the thickness of standard gauges. In the last stage, the trained ANN will return the value of the coating thickness and this parameter will be displayed on an HMI interface or screen. The system will be powered by a rechargeable battery and recharging will be through an external power supply. The portable device must work with thicknesses between 25 and 905 microns on 6061 aluminum and Zry-4. Consequently, this project will contribute to the research and development group "Non-destructive testing applied to the railway industry" of the Haedo Regional Faculty and to the industry that uses this measurement technique.
Graphical abstract
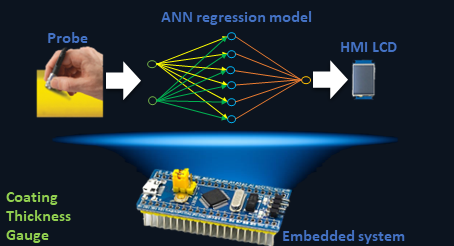
Actividades: 0 -
Ubicación
Grupo de Investigación en Inteligencia Artificial Aplicada
Universidad Tecnológica Nacional
Facultad Regional Haedo
Paris 532
Buenos Aires, Argentina
Teléfono: +54-011-4443-7466 (int. 144)
Fax: +54-011-4443-0499
Website: giiaa.frh.utn.edu.arActividades: 0
